dimanche 29 octobre 2017
vendredi 27 octobre 2017
Expressions rationnelles
Allo prof
Addition et soustraction d'expression rationnelle
Multiplier des expressions rationnelles
Division d'expressions rationnelles
henseignant
Addition (Soustraction) d'expressions rationnelles
Multiplication d'expressions algébriques rationnelles
Division d'expressions rationnelles
Daniel Bellerose
Réduire une expression rationnelle
Jeanne-d'Arc Cloutie
Addition et soustraction d'expressions rationnelle
Addition et soustraction d'expression rationnelle
Multiplier des expressions rationnelles
Division d'expressions rationnelles
henseignant
Addition (Soustraction) d'expressions rationnelles
Multiplication d'expressions algébriques rationnelles
Division d'expressions rationnelles
Daniel Bellerose
Réduire une expression rationnelle
Jeanne-d'Arc Cloutie
Addition et soustraction d'expressions rationnelle
lundi 16 octobre 2017
Factorisation
La factorisation permet de résoudre ce type de problème comme un jeu d'enfant.
On utilisera les tuiles algébriques pour faciliter l'intégration de la mécanique par une compréhension du pourquoi de la "méthode" somme et du produit.
 |
| source: Les figures de l'Ombre, film de Theodore Melfi, 2017 |
On a vu que le produit de 2 binômes est équivalent à calculer l'aire d'un rectangle ayant ces binômes pour mesure de ses côtés.
De plus, on observe que les produits des "diagonales" sont égaux 2x^2*(-15) = -30x^2 tout comme pour -3x*10x = -30x^2.
Donc pour la factorisation on se servira de cette propriété.
Cas #1: x^2 + Sx + P (aussi appeler somme-produit)
Dans ce cas nous remarquons que le coefficient du x^2 est 1.
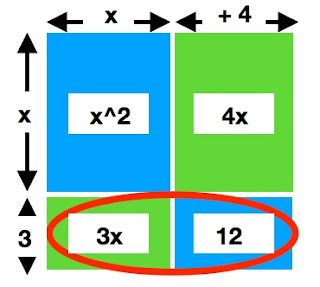
Voici un exemple de polynôme à factoriser : x^2 + 7x + 12. Comme on le voit dans la multiplication en haut les termes en x^2 et constants ne sont pas semblables à d'autres. Ainsi, nous les placerons aux extrémités.
On fait une mise en évidence pour la ranger de blocs supérieurs (x^2 et 4x). Ici ce sera "x" qui sera la mesure commune aux deux rectangle de cette rangée. Si x est la hauteur du rectangle x^2 alors sa largeur sera aussi x. De même pour le 4x, la largeur sera alors 4.
Pour la rangée du bas, nous avons déjà la largeur des rectangles écrits en haut (x et +4). Avec une dimension du rectangle, on cherche l'autre. Ayant la largeur x pour avoir une surface de 3x la hauteur sera 3. On peut valider 3*4 = 12
Voici un exemple de polynôme à factoriser : 2x^2 - 5x - 3. On fait la même chose. Puisque les termes en x^2 et constants ne sont pas semblables à d'autres, dans la multiplication, nous les placerons aux extrémités.
Donc pour la factorisation on se servira de cette propriété.
Cas #1: x^2 + Sx + P (aussi appeler somme-produit)
Dans ce cas nous remarquons que le coefficient du x^2 est 1.
Voici un exemple de polynôme à factoriser : x^2 + 7x + 12. Comme on le voit dans la multiplication en haut les termes en x^2 et constants ne sont pas semblables à d'autres. Ainsi, nous les placerons aux extrémités.
Donc on sait que le produite de la diagonale est 12x^2
Il manque le terme 7x pour avoir notre polynôme x^2 + 7x + 12
Quel sont les termes semblables dont le produit sera 12x^2 et la somme 7x?
Liste de facteurs pour 12x^2: 1x et 12x = 13x non, 2x et 6x = 8x non, 3x et 4x = 7x oui
Donc on aura...
On fait une mise en évidence pour la ranger de blocs supérieurs (x^2 et 4x). Ici ce sera "x" qui sera la mesure commune aux deux rectangle de cette rangée. Si x est la hauteur du rectangle x^2 alors sa largeur sera aussi x. De même pour le 4x, la largeur sera alors 4.
Pour la rangée du bas, nous avons déjà la largeur des rectangles écrits en haut (x et +4). Avec une dimension du rectangle, on cherche l'autre. Ayant la largeur x pour avoir une surface de 3x la hauteur sera 3. On peut valider 3*4 = 12
Donc la factorisation du polynôme x^2 + 7x + 12 = (x+4) (x+3).
Cas #2: ax^2 + bx + c (cas beaucoup plus fréquent, cas #1 est un particulier du cas #2)
Voici un exemple de polynôme à factoriser : 2x^2 - 5x - 3. On fait la même chose. Puisque les termes en x^2 et constants ne sont pas semblables à d'autres, dans la multiplication, nous les placerons aux extrémités.
Donc on sait que le produite de la diagonale est -6x^2
Il manque le terme -5x pour avoir notre polynôme 2x^2 - 5x - 3
Quel sont les termes semblables dont le produit sera -6x^2 et la somme -5x?
Tout d'abord remarquez que le produit est négatif, donc un terme sera positif et l'autre négatif.
Remarquez aussi que la somme (-5x) est négative. Donc le plus grand facteur sera celui de négatif.
Liste de facteurs pour -6x^2: 1x et -6x = -5x oui
2x et -3x = -x non
On fait une mise en évidence pour la ranger de blocs du haut (2x^2 et -6x). Ici ce sera "2x" qui sera la mesure commune aux deux rectangles de cette rangée. Si 2x est la hauteur du rectangle 2x^2 alors sa largeur sera x. De même pour le -6x, la largeur sera alors -3.
Pour la rangée du bas, nous avons déjà la largeur des rectangles écrits en haut (x et -3). Avec une dimension du rectangle, on cherche l'autre. Ayant la largeur x pour avoir une surface de x la hauteur sera 1. On peut valider avec l'autre rectangle -3*1 = -3
Donc la factorisation du polynôme 2x^2 -5x - 3 = (x-3) (2x+1).
Devoir:
p.59 # 18 et 19
mardi 10 octobre 2017
Mise en évidence simple ou double
Allo prof
Mise en évidence simple
Mise en évidence double
henseignant
Mise en évidence double
Virginie Fillion
Mise en évidence simple
Carl Grandmont
Mise en évidence simple
Mise en évidence double
Mise en évidence simple
Mise en évidence double
henseignant
Mise en évidence double
Virginie Fillion
Mise en évidence simple
Carl Grandmont
Mise en évidence simple
Mise en évidence double
jeudi 5 octobre 2017
Multiplication avec tuiles algébriques
Bonjour,
Voici les réponses des 5 multiplication données en devoir.
a) 9x^2 - 16
b) 4x^2 - 28x + 49
c) 6x^3 - 11x^2 - 18x + 20
d) 2x^2 + 10x - 28
e) -6x^2 + 7x + 20
Voici un vidéo qui rappel la multiplication algébrique
Voici les réponses des 5 multiplication données en devoir.
a) 9x^2 - 16
b) 4x^2 - 28x + 49
c) 6x^3 - 11x^2 - 18x + 20
d) 2x^2 + 10x - 28
e) -6x^2 + 7x + 20
Voici un vidéo qui rappel la multiplication algébrique
S'abonner à :
Commentaires (Atom)